Три сосны
Mar. 2nd, 2026 11:34 pmПоляна первая: דְּרָקוֹן, דַּרְכּוֹן и דַּקְרוֹן (дарко́н, драко́н и дакро́н)
1. Дарко́н - דַּרְכּוֹן - "паспорт". Происходит от слова דֶּרֶךְ (дэ́рэх) "дорога". Слово весьма известное даже тем, кто вообще никакого отношения к Израилю не имеет. Это такая синерожая паспортина, с которой можно ездить без проблем почти по всему земному шару (ну, кроме арабских стран). И почти каждый русскоязычный человек, когда впервые сталкивается с этим словом, начинает производить очевидные шутки на тему схожести со словом "дракон". Это нормально.
2. Драко́н - דְּרָקוֹן. Да, такое слово тоже есть в иврите, формально происходит из греческого. Но появилось в языке, конешно, в новые времена - с изучением мифологии народов мира. Пишется оно через другую букву: вместо кафа там куф, как и ожидается от иностранных слов.
3. Дакро́н - דַּקְרוֹן. Это название торговой марки для синтетической ткани, которое известно во всём мире. Изобретено в 1941 году во Франции. Ткань раньше применялась для всего - в одежде, в обивках, в простынях-шторах и снаряжении. Сейчас не так популярна, потому что не разлагается в природе. В Израиле тоже было время, когда вся одежда была из дакрона.
В фильме "Высота Хальфон не отвечает" героиня, одетая в леопардовый африканский наряд, пытается соблазнить одного комического персонажа - мол, не жарко ли тебе? А тот ей отвечает:
חם חם. נורא חם פה. לך בטח לא כל כך חם עם הדקרון הזה. הא? זה חומר טוב זה.
"Жарко, жарко. Тут ужасно жарко. Тебе-то, конешно, не так жарко с этим дакроном, а? Хорош матерьяльчик".
( Поляна вторая )

Мечистый Лев
Mar. 2nd, 2026 11:29 pm"Пресс-секретарь ЦАХАЛа сообщил о начале операции Мечистый Лев Весь в Огне Такой и Чешуя Везде и Демоны Ревущие".

ну GPT, конешно, после долгих итераций и с фотошопными правками
Thoughts and Prayers!
Mar. 2nd, 2026 12:54 pmFirst lady Melania Trump expressed condolences to families who have lost loved ones to death and injury during an address to the United Nations on Monday that described “these challenging times.”
In an unprecedented role for a first lady, she opened a meeting of the U.N. Security Council on behalf of the U.S. as the country assumed the rotating presidency of the council. “I extend my earnest wishes for a swift and smooth recovery to all those who have been injured. You are in my thoughts and prayers during these challenging times,” Trump said, without mentioning any particular conflict.
https://www.wsj.com/livecoverage/iran-israel-us-strikes-2026/card/speaking-at-un-melania-trump-expresses-condolences-for-the-dead-4oUsYCq5A2LzcAeEHn9Z
It's like watching a really bad movie about geopolitics.
Clout Debt
Mar. 2nd, 2026 07:43 pmZXC 0.8.0 и 0.8.1
Mar. 2nd, 2026 07:36 pmСостоялся выпуск 0.8.0 библиотеки и кроссплатформенной консольной утилиты ZXC (github.com), реализующих высокопроизводительное многопоточное асимметричное сжатие без потерь и оптимизированное для игровых ресурсов, прошивок и пакетов приложений.
Декларируется на 40%+ более быстрая распаковка, чем LZ4 на ARM64, с лучшими коэффициентами сжатия.
( читать дальше... )
флорентин
Mar. 2nd, 2026 02:21 pm«В эту субботу началась вторая война с Ираном, и я оказался в Тель-Авиве. Мне показалось, что это подходящий момент сыграть в шахматы.
Дело в том, что во время ковида я вступил в шахматную группу во Флорентине. С тех пор она разрослась более чем до 700 участников, и люди постоянно собираются поиграть в месте под названием “Malabiya”, в самом сердце района.
В этот военный день “Malabiya” была закрыта. Но Эммануэль и Рои, двое завсегдатаев, стояли снаружи. Я присоединился к ним, и мы устроились на скамейке, отогнав пару бездомных, чтобы освободить место.
Каждые пятнадцать минут звучала сирена воздушной тревоги. Я придумал глупое, но смелое правило: кто встанет и побежит в убежище, тот проигрывает по времени. В шахматном клубе “Malabiya” часы не останавливаются из-за воздушных атак 🙂
В какой-то момент к нам подошёл прохожий. Он сказал, что он из Киева и что восхищается тем, что мы играем несмотря ни на что…»

Стефан Цвейг, "Амок"
Mar. 2nd, 2026 01:09 pm"...Но на следующий день он (клерк) сообщил мне приятную новость, что еще может занять для меня одну каюту, правда не особенно комфортабельную, под палубой и в средней части парохода. Я с нетерпением стремился домой, поэтому, не долго думая, попросил закрепить за мной место.
Клерк правильно осведомил меня. Пароход был переполнен, а каюта плохая - тесный четырехугольный закуток недалеко от машинного отделения, освещенный только тусклым глазом иллюминатора. В душном, застоявшемся воздухе пахло маслом и плесенью; ни на миг нельзя было уйти от электрического вентилятора, который, как обезумевшая стальная летучая мышь, вертелся и визжал над самой головой. Внизу машина кряхтела и стонала, точно грузчик, без конца взбирающийся с кулем угля по одной и той же лестнице; наверху непрерывно шаркали шаги гуляющих по палубе. Поэтому, сунув чемодан в этот затхлый гроб меж серых шпангоутов, я поспешил на палубу и, поднимаясь по трапу, вдохнул, как амбру, мягкий, сладостный воздух, доносимый к нам береговым ветром.
Но и наверху царили сутолока и теснота: тут было полно людей, которые с нервозностью, порожденной вынужденным бездействием, без умолку болтая, расхаживали по палубе. Щебетание и трескотня женщин, безостановочное кружение по тесным закоулкам палубы, назойливая болтовня пассажиров, скоплявшихся перед креслами, - все это почему-то причиняло мне боль..."
(no subject)
Mar. 1st, 2026 06:59 pm
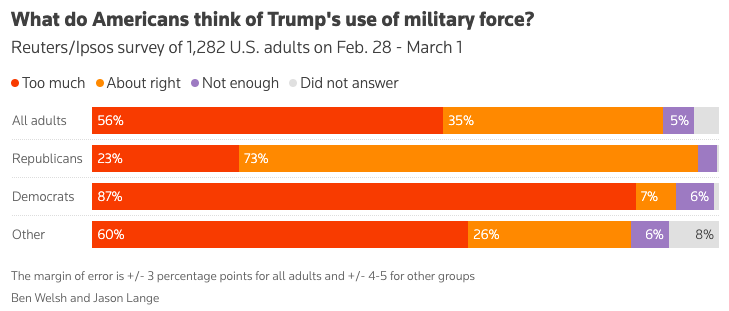
https://www.reuters.com/world/us/just-one-four-americans-support-us-strikes-iran-reutersipsos-poll-finds-2026-03-01/
As before, Republicans are opposite of Independents, not Democrats.
Кілька новин поруч
Mar. 2nd, 2026 02:25 amhttps://censor.net/ua/n3602976
Президент Кіпру Нікос Христодулідіс заявив, що він розмовляв з прем'єр-міністром Великої Британії Кіром Стармером, який підтвердив, що Кіпр не є ціллю для Ірану
https://censor.net/ua/n3603000
На британській авіабазі "Акротірі", що розташована в кіпрському Лімассолі, зафіксовано ймовірну атаку після повідомлень про невдалі удари Ірану на острів
https://censor.net/ua/n3603047
*
Британія хоче залучити фахівців з України для збиття іранських дронів у Перській затоці, - Стармер
https://censor.net/ua/n3603041
More frog
Mar. 2nd, 2026 07:45 amAs soon as the tadpoles started growing legs they changed rapidly. Within days the kinda dopey goldfish behaviour, like nibbling around the surface of the water, disappeared, they became very elusive and shy. Almost like as soon as they started thinking about being predators they realised they were also prey. It was a bit sad, because I really enjoyed watching them, but also necessary for them to become wild frogs. I was glad that I hadn't spoiled them for life on their own.
( Read more... )
waterfall
Mar. 1st, 2026 07:00 pm(no subject)
Mar. 1st, 2026 09:57 amIsraeli and U.S. military intelligence had long watched and waited for a rare opportunity: senior political and military leaders in Iran holding a meeting—where they could all be killed at once.
The day finally came Saturday.
Intelligence officers had identified not just one meeting but three, Israeli officials said. And they had a fix on Supreme Leader Ayatollah Ali Khamenei, Iran’s top decision maker and spiritual leader.
The moment was so unique that U.S. and Israeli warplanes struck in full daylight. Israeli jets dropped 30 bombs on Khamenei’s compound leaving it scorched and shattered.
https://www.wsj.com/world/middle-east/why-the-u-s-and-israel-struck-iran-when-they-did-a-chance-to-kill-its-leaders-b0dbbc88
Trump started the war because he had an opportunity to kill Khamenei. That's all.
фейсбук
Mar. 1st, 2026 07:25 pmЧестно говоря, сразу подумал, что наверное умер. Или разругался со всеми и уехал куда-то... но скорее все-таки умер. День-два ничего с этим не делал, а потом все-таки пересилил неловкость и пишу его близкому другу: привет, давно не виделись, слушай, извини, если это неловкий вопрос, а помнишь вот Н.? Я с тех пор его не встречал, недавно толкнуло вдруг - как он, что он, если ты в курсе, расскажи?
Оказалось... оказалось, что все хорошо у него. Живет в Израиле, семья, двое детей почти уже взрослых. Работает в такой-то большой компании, с этим самым близким другом до сих пор дружит и периодически вместе в отпуск ездят семьями. Все у него хорошо.
Просто не в фейсбуке.
Шва на
Mar. 1st, 2026 03:22 pmС другой стороны у нас есть слабый дагеш, который проявляется в шести буквах בגד כפת ("бегед кефет"), если они стоят в начале слова или идут после закрытого слога. Из-за этого, например, три буквы из этого списка - בכפ - изменяют своё звучание на взрывное ("б", "к", "п"). Ну, это азы.
Пока это хорошо объясняет, почему, например, слово בַּרְבּוּר "лебедь" читается как "барбу́р" - с двумя звуками "б". Потому что первый слог "бар" - закрытый. Его запирает "шва покоящееся".
Но не объясняет, скажем, простое слово כּוֹתְבִים "пишут", которое читается, как "котви́м". Вроде там же шва стоит, слог должен закрываться, а "в" превращаться в "б". Но нет.
А оказывается, там под тавом стоит как раз "шва движущееся", а оно слог не запирает. И 5000 лет назад это слово звучало, как "котэви́м" (и даже в середине XX века у израильских дикторов по радио). В итоге слог не закрытый, дагеш не появляется. Древнее звучание слов удивительным образом проявляется в современной системе огласовок.
Есть для этого случая и отдельное правило: шва будет движущимся после полной огласовки. Полной огласовкой тут работает холам малэ - וֹ (полный холам).
Вот как раз недавно мы с друзьями тут зарубились по поводу слова אֵימְתָן (эймэта́н) "страхолюдина". Меня запутал ИРИС, и я был уверен, что там первый слог закрытый. Но ИРИС иногда врёт. А правило всё равно работает - здесь полный цэрэ (с йудом) и дальше идёт шва движущееся. В итоге три чётких слога и никакого дагеша в таве.
Такой же вышеописанный кунштюк происходит в том же паале и в прошедшем времени - כָּתְבה ("катва́", а не "катба" - "она писала"). И тоже есть своё правило для этого случая - шва будет движущимся после большой безударной огласовки в середине слова. Камац под кафом - это именно большая огласовка. Тоже древнее звучание. А вот пааль в инфинитиве без всяких засад - לִשְׁבּוֹר, шва покоящееся закрывает слог, дагеш в бете.
Я постоянно открываю эту америку через разные форточки, сплошной сквозняк.

Сергій Косяк, 1 березня 2014 року
Mar. 1st, 2026 02:17 pmЗі щоденника Сергія Косяка (1975), українського громадського активіста, у березні 2014 р. – мешканця Донецька, пастора церкви християн віри євангельської «Асамблея Божа», ініціатора міжконфесійного молитовного марафону «Молитва за Україну»:
Був сьогодні на мітингу біля Донецької ОДА, а потім поїхав на площу Леніна, котра стала місцем дислокації сепаратистів. Влада розгойдувала маховик «антифашизму» і «антибандерівщини», який вже не можуть зупинити. Люди збожеволіли, підігріті антиукраїнськими ораторами, ненавидять усіх, на кого їм укажуть «крикуни». Багатотисячний розбурханий натовп з площі Леніна рушив брати Донецьку ОДА.
Божевілля, інших слів немає... Здається, зібралося таке бидло, що будь-кого на вила візьмуть.
Я перебував на сходах перед будівлею обладміністрації і попросив дати мені мікрофон. Приблизно 5 хвилин закликав людей до молитви про мир, але вони оскаженіло горлали, не реагуючи на мої заклики. А під час хвилини мовчання про загиблих у сутичках у Києві скандували: «Беркут!».
У цих людей немає нічого святого, тільки ненависть натомість. Було добре помітно, що всім цим безладом хтось керує і основна мета – це дестабілізація і розпалювання агресії.
Коли я йшов від облдержадміністрації, було чутно, як вибухають світлошумові гранати. Це міліція відбивалася від натовпу, що йшов на штурм будівлі.
(Сергій Косяк, Донбас, якого ти не знав. Щоденник священника. Книга перша, переклад з російської Ірини Кримської (Київ: Видавець Заславський О. Ю., 2021), с. 14)
а вот ещё Feuer!
Mar. 1st, 2026 05:50 am"У кенигсбергских зажиточных жительниц есть обыкновение в зимнее холодное время носить с собою в церковь особливые медные и наподобие плоских ларчиков сделанные сосудцы, наполненные жаром. Сии сосудцы, или согревательницы, усевшись в своих лавках, становят они у себя под ноги и под подол, и как они и сверху и с сторон делаются скрытыми, то опасности от огня быть не может, а тепла производят они собою много и согревают с избытком нежных пруссачек. Сим образом было и в сей раз множество женщин с таковыми точно медными и прекрасными коробочками, наполненными жаром, в сей кирке. И неизвестно уже заподлинно, по какому собственно поводу случилось одной из сих женщин, сидевшей посреди самой церкви во время продолжения проповеди, которую слушали все с великим вниманием, обратиться к соседке своей и, заворошившись, молвить словцо «фейер», что на нашем языке собственно значит «огонь». Обожглась ли она о свою коробочку, растворилась ли она и высыпался ли из ней жар, или так хотела она соседке сказать, что огонь в коробочке ее потух, — всего того заподлинно неизвестно, да и допытаться того в точности после не могли; а довольно только того, что упомянутое выговоренное ею словцо услышали многие и другие, и из единого любопытства стали друг у друга расспрашивать, что б такое сделалось, и повторять словцо сие в тихих разговорах между собою. Как произошло от того небольшое шушуканье и друг у друга спрашивание, то к, особливому несчастию, и разнеслось слово сие в единый миг по всей церкви, и весь народ начал твердить: "Фейер! Фейер!""
Когда я однажды шабашил в Берлине, часа в четыре дня немцы собирались все на что-то вроде шоу - звали меня, чтобы я сел играть в какую-то игрушку, где надо было мочить фрицев - я играл в честную, без читинга - и они стояли сзади и подсказывали, крича Feuer, Feuer! И я лупил из чего-то по фашистам.